#Quadratic vertex form plus
We were able to show this is a graph of the quadratic equation ๐ฆ is equal to negative one times ๐ฅ plus seven all squared. We divide both sides of the equation through by four to get that ๐ is equal to negative one.ฤฏinally, we just substitute ๐ is equal to negative one into the vertex form to find the equation of this graph. This gives us negative four is equal to four ๐. So we get negative four is equal to eight times two squared. We have that negative five plus seven is equal to two. And now all thatโs left to do is simplify and rearrange to solve for the value of ๐.
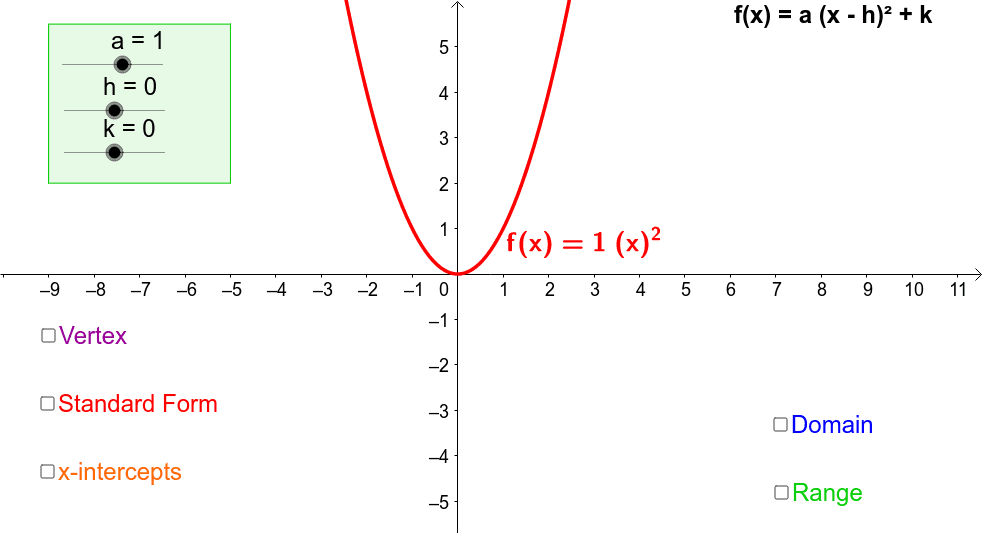
We get negative four is equal to ๐ times negative five plus seven all squared. So we substitute these coordinates into the equation for our graph. A quadratic in standard form can be expressed in vertex form by completing the square.
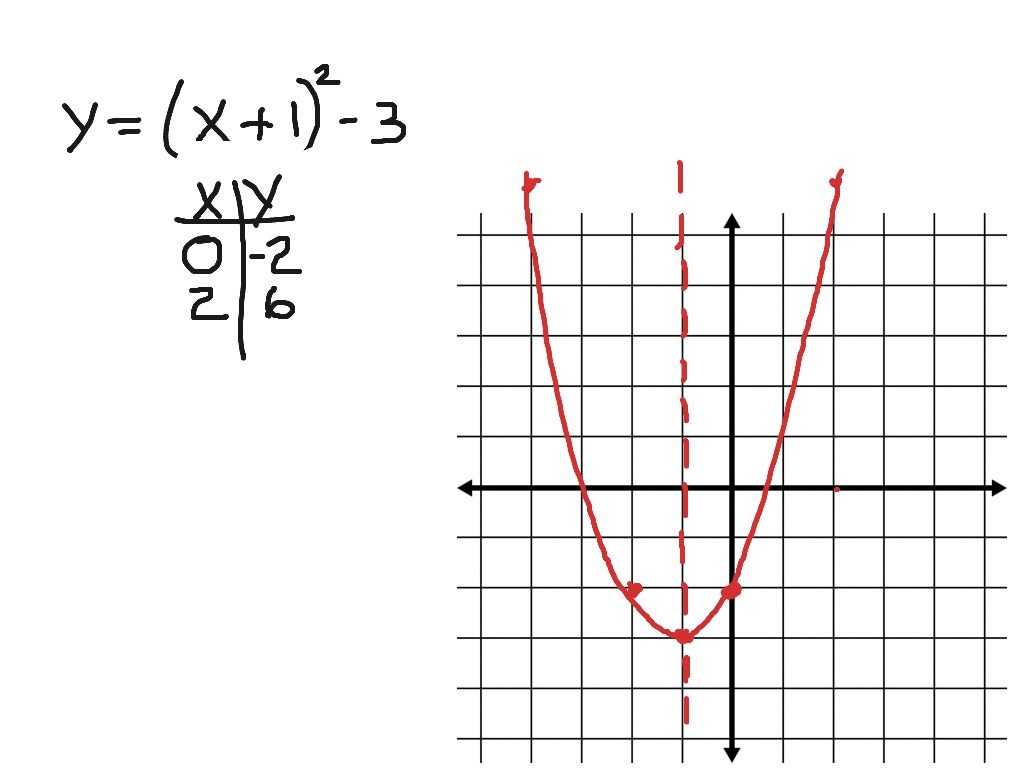
Example: Convert the quadratic function f(x) 2x 2 - 8x + 3 into the vertex form. A quadratic function f(x) ax 2 + bx + c can be easily converted into the vertex form f(x) a (x - h) 2 + k by using the values h -b/2a and k f(-b/2a).
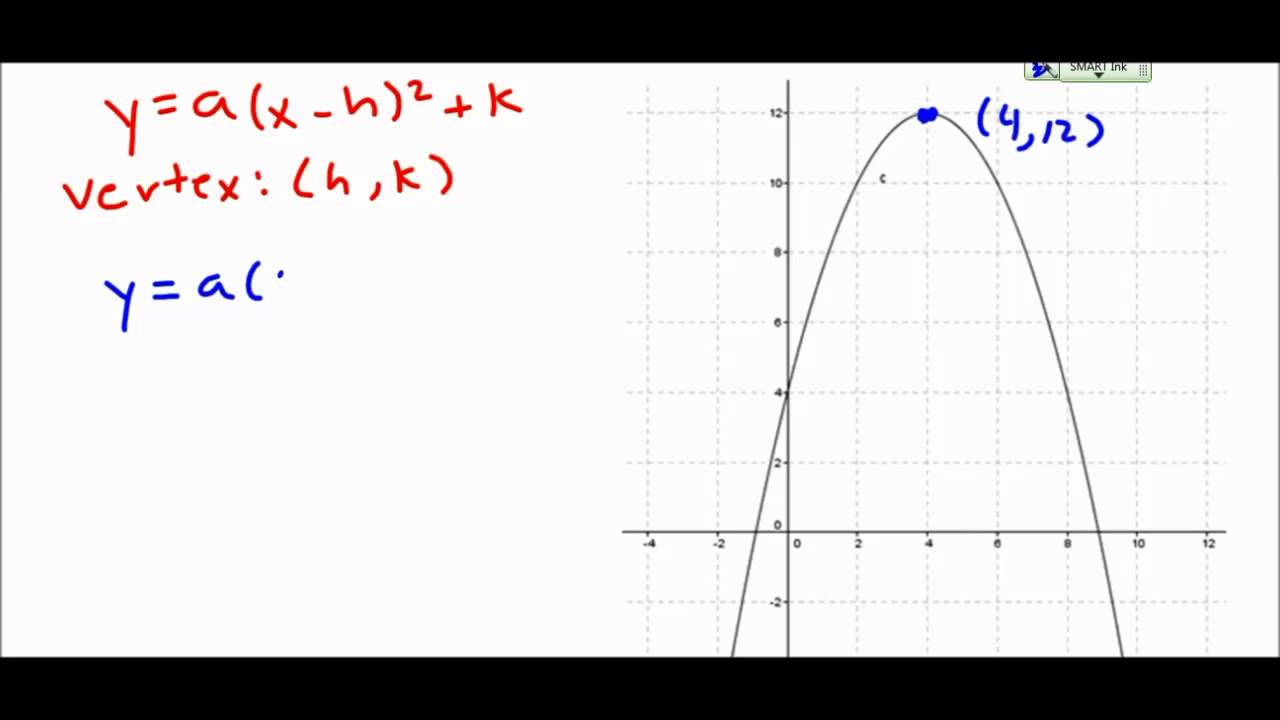
We can find one such point with coordinates negative five, negative four. Converting Standard Form of Quadratic Function Into Vertex Form. And when choosing this point, we should choose a point with integer coordinates, since then we can be accurate. And to do this, weโre going to need the coordinates of a point which lies on the line. This gives us ๐ฆ is equal to ๐ times ๐ฅ minus negative seven all squared plus zero, which we can simplify to give us ๐ฆ is equal to ๐ times ๐ฅ plus seven all squared. In a quadratic equation, the term a, the term b, and the constant term (the term without a variable) c. Method 1 Using the Vertex Formula 1 Identify the values of a, b, and c. To do this, letโs first substitute โ is negative seven and ๐ is equal to zero into the vertex form. If you want to find the vertex of a quadratic equation, you can either use the vertex formula, or complete the square. The only unknown left in the vertex form is the value of ๐. Therefore, weโve determined the values of both โ and ๐. Therefore, since we found the coordinates of the vertex to be negative seven, zero, we know โ must be negative seven and ๐ must be zero. And this is because for a quadratic equation given in vertex form, the coordinates of the vertex will be โ, ๐. If, like in equation (1.) above, the signs in the equation match that of the generalized vertex form, then we. In this case, we can see the coordinates of this point are negative seven, zero.ฤชnd since we can determine the coordinates of the vertex of this graph, it will be easier to work with the vertex form. We need to remember the vertex form a(x - h)2 + k. Or alternatively, since this curve opens downwards, it will be the maximum value for the output. And remember, this is the point on the curve where the line of symmetry passes through. However, a good rule of thumb is to check what the coordinates of the vertex of the graph is. And there are positives and negatives to choosing either. The first of these is called the standard form for a quadratic equation, and the second is called the vertex form. We can write this in the form ๐ฆ is equal to ๐๐ฅ squared plus ๐๐ฅ plus ๐ or ๐ฆ is equal to ๐ times ๐ฅ minus โ all squared plus ๐, where ๐, ๐, ๐, โ, and ๐ are real numbers and ๐ is not allowed to be equal to zero. And to do this, weโll start by recalling thereโs two ways we can represent the graph of a quadratic function. And we need to determine the quadratic equation which is represented by this graph. In this question, weโre given the graph of a function. This article was written for you by Jeremie, one of the tutors with Test Prep Academy.Write the quadratic equation represented by the graph shown. Looking to get ready for the SAT? We can help with SAT Prep Thus we can tell there are no real roots because the vertex is above the x-axis and the parabola opens upwards. So our quadratic in vertex form is y = 3(x + 2) 2 + 3 and the vertex can be found at (-2, 3).ฤชdditionally we can see that the quadratic opens upwards because the value of both a and m are positive.
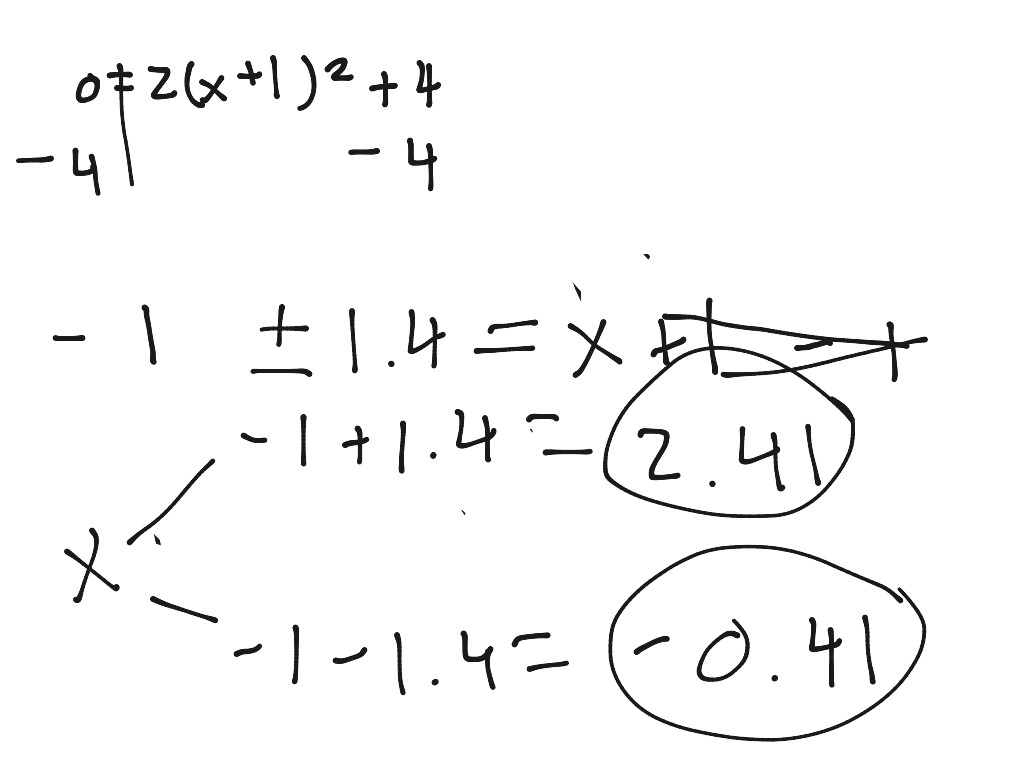
Step 3: Add and subtract that value inside the brackets to keep the function the same. Step 2: Calculate 0.25b 2 where b is the coefficient of x. The other two numbers can be anything as the number in the parentheses affects. Step 1: Factor out the coefficient of x 2 from the first two terms. The constant at the end is the value that affects the maximum. Complete the square of y = 3x 2 + 12x + 15 To take a quadratic in the form y = ax 2 + bx + c and factor it into y = m(x โ s) 2 + t, we must complete the square. This form is used to easily find the vertex of a quadratic which can be found at point (s, t). The vertex form of a quadratic has the form y = m(x โ s) 2 + t for some m, s and t.
0 kommentar(er)
